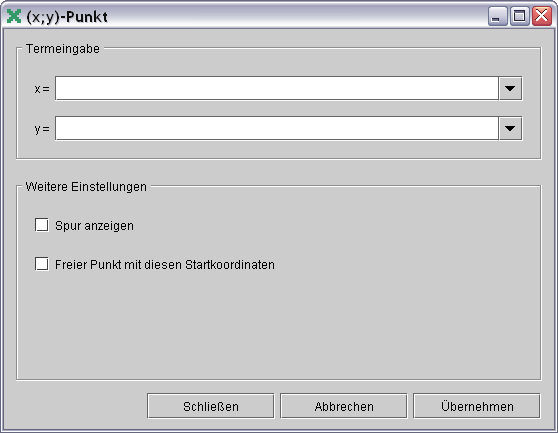
(x;y)-Punkt
- Term fⁿr die x-Koordinate
- Term fⁿr die y-Koordinate
- Punkt
Dem
 (x;y)-Punkt
(x;y)-Punkt auch Punkte erzeugen, die nicht mit Zirkel und Lineal konstruierbar sind.
auch Punkte erzeugen, die nicht mit Zirkel und Lineal konstruierbar sind.
Nachdem in der Konstruktionsleiste  (x;y)-Punkt
(x;y)-Punkt (x;y)-Punkt
(x;y)-Punkt
Beispiele
- x = 2
y = X(A) - x = Sin(X(A))+Cos(Y(B))
y = If(X(A)<0,4,Y(A)+2)
Weitere Informationen sind unter
Wurden bereits Terme eingegeben, so kann auf diese in den Auswahllisten der Eingabe-Felder zugegriffen werden.

Spuren
Vor allem bei berechneten Punkten ist eine Spur von besonderer Bedeutung (Plotter). Deshalb bietet der Eingabe-Dialog durch das KontrollkΣstchen "Spur anzeigen" die M÷glichkeit, dem zu erzeugenden  (x;y)-Punkt
(x;y)-Punkt
Freie Punkte mit Startposition
Der Dialog  (x;y)-Punkt
(x;y)-Punkt (x;y)-Punkt
(x;y)-Punkt
Ein freier Punkt kann auch nachtrΣglich im Dialog  Objekteigenschaften
Objekteigenschaften
Bedingte Punkte
(x;y)-Punkte k÷nnen auch als bedingte Punkte eingesetzt werden. Dazu mⁿssen den Koordinaten Bedingungen (If(bedingung,wahr,falsch)) zugewiesen werden.
Beispiel
x-Koordinate If(X(A)<0,0,X(A))
y-Koordinate If(X(A)<0,0,-Y(A))
Der entstehende  (x;y)-Punkt
(x;y)-Punkt
Siehe auch: